따릉이 데이터 분석하기 (4) Transformation
따릉이 데이터 분석하기 (4) Transformation
이번에는 PCA를 비롯해 예측변수의 데이터셋을 변환시키는transformation 여러 가지 방법들에 대해 다루어보도록 하겠다. 대표적으로 PCA는 기본적인 회귀문제에 응용되어 PCR로 사용되거나, 고차원 문제의 차원 축소 기법으로 필수적인 역할을 한다. 여기서는 우선 PCA를 진행하고, 이 결과를 바탕으로 PCR을 진행하여 이를 PLS와 비교해보도록 하자.
PCA
PCA는 scikit-learn의 sklearn.decomposition.PCA를 이용하도록 하겠다. 다만, data transformation에서는 data의 scale이 중요하기 때문에 StandardScaler()을 이용해 데이터를 표준화시킨 후 PCA를 진행하도록 하겠다. 이를 위해 이번에는 Pipeline이라는 scikit-learn의 툴을 이용해 일련의 전처리과정부터 PCA까지를 도식화하고 가시적으로 유용한 모델을 만들어보도록 하겠다(Pipeline은 scikit-learn의 꽃이니 반드시 사용 테크닉을 익히도록 하자😃).
우선 필요한 모듈들을 다음과 같이 로드하도록 하자.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
from sklearn.pipeline import Pipeline
from sklearn.compose import ColumnTransformer
from sklearn.impute import SimpleImputer
import statsmodels.api as sm
np.random.seed(37)
Data load의 과정은 이전에 했던 것과 유사하지만, NA 값을 버리지 않고 추후 Imputer를 이용해 결측값을 median중간값으로 처리할 것이므로, dropna()를 배제했으며, train_test split 이전에 우선 예측변수와 반응변수를 각각 데이터프레임, 벡터로 분리했다. 코드는 다음과 같다,
# Data Load
df_train = pd.read_csv('train.csv')
df_train = df_train.iloc[:,1:]
df_train.columns = ['hour', 'temp', 'precip',
'windspeed', 'humidity', 'visibility',
'ozone', 'pm10', 'pm2_5', 'count']
df_X = df_train[df_train.columns.drop('count')]
df_y = df_train['count'].values
이를 바탕으로, 데이터를 전처리하는 preprocessor를 만들고, 이를 PCA 모듈과 이어지게 하는 파이프라인을 구성할 것인데, 이 과정에서 scikit-learn의 ColumnTransformer() 모듈을 이용하도록 할 것이다. 이는 특정 열(feature)들에 대해 서로 다른 전처리 과정을 적용할 수 있도록 하는데, 현재 다루고자 하는 데이터에서는 precip 변수(categorical_features)는 0/1로 코딩되어있으므로 OneHotEncoder를 적용해야 하고 나머지 변수에 대해서는 StandardScaler()을 적용해야 한다. 이때 개인적으로 시간대를 나타내는 hour 변수를 별도로 처리해야한다고 생각해 hour_feature로 분리했는데, StandardScaler로 처리하는 preprocessor_1과 hour 전체를 One-hot encoding으로 처리하는 preprocessor_2를 만들어 비교해보도록 할 것이다(이때, hour가 취하는 값이 24개이므로 sparse matrix가 생성되는데, 이 경우 PCA방법이 달라져야 하므로 여기서는 sparse=False로 설정했다). 코드는 다음과 같다.
# Data Preprocessing
numeric_features = list(df_X.columns.drop(['precip','hour']))
numeric_transformer = Pipeline(
steps=[("imputer",SimpleImputer(strategy='median')),("scaler",StandardScaler())]
)
hour_feature = ['hour']
hour_transformer = Pipeline(
steps=[("imputer",SimpleImputer(strategy='most_frequent')),('scaler',StandardScaler(with_std=False))]
) # hour은 standardscaler에서 표준편차로 나누는 것은 제외함.
hour_transformer_oh = OneHotEncoder(handle_unknown='ignore',sparse=False) # hour을 onehotencoding으로 처리, sparse=False는 sparse matrix로 반환하지 않게 설정
categorical_features = ['precip']
categorical_transformer = OneHotEncoder(handle_unknown='ignore')
preprocessor_1 = ColumnTransformer(
transformers=[
("num", numeric_transformer, numeric_features),
('hour', hour_transformer, hour_feature),
("cat", categorical_transformer, categorical_features)
]
)
preprocessor_2 = ColumnTransformer(
transformers=[
("num", numeric_transformer, numeric_features),
('hour', hour_transformer_oh, hour_feature),
("cat", categorical_transformer, categorical_features)
]
)
scikit-learn에는 이러한 Pipeline 객체를 html 형태로 도식화해주는 set_config메서드가 있다. 아래와 같이 설정하면 된다.
# Visualize Pipeline
from sklearn import set_config
set_config(display="diagram")
이후 PCA와 preprocessor_1,2 를 각각 합쳐 각각의 새로운 Pipeline pca_1,pca_2로 만들었다. 이후 Training data set을 이전에 사용한 train_test_split 메서드를 이용해 train data와 validation data로 나누었으며, validation 비율은 마찬가지로 30%를 적용했다. 그리고 train data로 각각의 Pipeline을 학습시켰다(fit method, 아래 코드 참고).
# Principal Component Regression by pipeline
pca_1 = Pipeline(
steps=[("preprocessor",preprocessor_1),("pca",PCA())]
)
pca_2 = Pipeline(
steps=[("preprocessor",preprocessor_2),("pca",PCA())]
)
X_train, X_val, y_train, y_val = train_test_split(df_X, df_y, test_size=0.3, random_state=0)
pca_1.fit(X_train,y_train)
pca_2.fit(X_train,y_train)
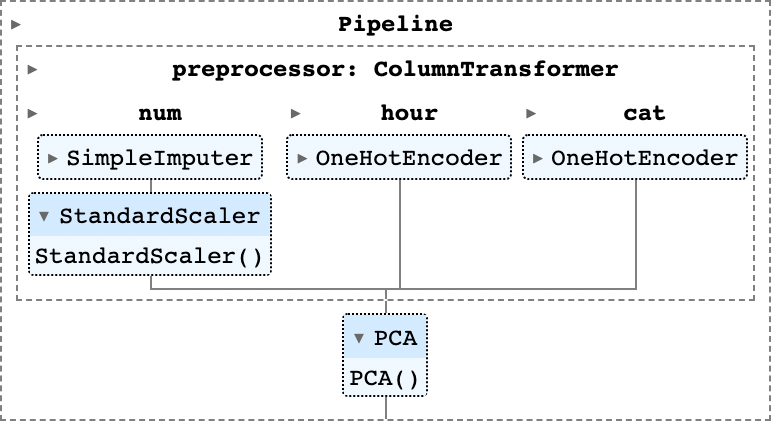
그러면 위와 같이 Interactive한 html 객체가 나오는데, 각 항목을 클릭하면 적용된 각 메서드에 대해 hyperparmeter나 설정을 어떻게 취했는지 파악할 수 있다. 이제 PCA가 적용된 결과를 파악해보도록 하자. Pipeline의 각 단계와 해당 단계에서의 attribute는 리스트로 저장되고 Pipelline 형성 단계에서 설정한 각 단계의 이름으로 이를 불러올 수 있는데(.named_steps['이름'] attribute 이용), 아래와 같이 pca_1,pca_2에서의 explained_variance_ratio를 파악할 수 있다. 이는 각 주성분이 전체 분산의 얼마만큼의 비율을 설명하는지 의미한다.
다음 코드를 통해 생성한 데이터프레임 pca_res는 각 PCA pipeline 모델(Scaler : StandardScaler를 적용한 pca_1, One-hot : OneHotEncoder를 적용한 pca_2)의 첫번째~10번째 주성분이 설명하는 전체 데이터의 분산비율을 의미한다(결과는 아래 표).
# PCA result
pca_step_1 = pca_1.named_steps['pca'] # load pca step for pca_1
pca_1_ratio = pca_step_1.explained_variance_ratio_.round(3)
pca_step_2 = pca_2.named_steps['pca'] # load pca step for pca_2
pca_2_ratio = pca_step_2.explained_variance_ratio_.round(3)
pca_res = pd.DataFrame([pca_1_ratio,pca_2_ratio], index=['Scaler','One-hot'], columns=range(1,11,1)).T
pca_res.iloc[:3,:].sum(axis=0) # Ex.ratio of first three components
\vert \vert Scaler \vert One-hot \vert \vert —: \vert —–: \vert ——: \vert \vert 1 \vert 0.884 \vert 0.336 \vert \vert 2 \vert 0.039 \vert 0.232 \vert \vert 3 \vert 0.031 \vert 0.105 \vert \vert 4 \vert 0.015 \vert 0.080 \vert \vert 5 \vert 0.012 \vert 0.055 \vert \vert 6 \vert 0.008 \vert 0.049 \vert \vert 7 \vert 0.007 \vert 0.021 \vert \vert 8 \vert 0.003 \vert 0.008 \vert \vert 9 \vert 0.001 \vert 0.006 \vert \vert 10 \vert 0.000 \vert 0.006 \vert
이를 보면 One-hot encoding을 처리하지 않은 첫번째 PCA 모델이 더 효과적으로 주성분 분리가 일어났음을 확인할 수 있는데, pca_res.iloc[:3,:].sum(axis=0) 코드로 처음 세 개의 주성분이 설명하는 비율을 확인해보면 Scaler는 95.4%, One-hot은 67.3% 이다. 따라서, PCR과 PLS를 비교하는 과정에서는 preprocessor_1만 이용하고, PCA 단계에서는 3개의 주성분을 사용하도록 하겠다.
Principal Component Regression & Partial Least Squares
PCR주성분회귀은 예측변수행렬의 고유값분해를 기반으로 회귀계수를 추정하는 방법이다(참고). 즉, PCA를 training data에 적용시킴으로써 차원 축소가 가능하게 하고, 이를 바탕으로 선형 회귀를 진행하는 것이다. 이때 PCA는 반응변수에 무관하게 작동하므로, unsupervised transformation이 일어난다고 볼 수 있다.PLS는 Linear regression 알고리즘의 일종인데, PCR과 유사하게 예측변수 열벡터들의 선형결합을 바탕으로 선형 모형을 구성하지만, 그 과정에서 반응변수와의 관계가 개입되므로 supervised transformation이라는 것이 PCR과의 차이점이다.
PCR
# PCR
from sklearn.linear_model import LinearRegression
pcr = Pipeline(
steps=[('Preprocessor',preprocessor_1),
('PCA',PCA(n_components=3)),
('Linear',LinearRegression())]
)
pcr.fit(X_train, y_train)
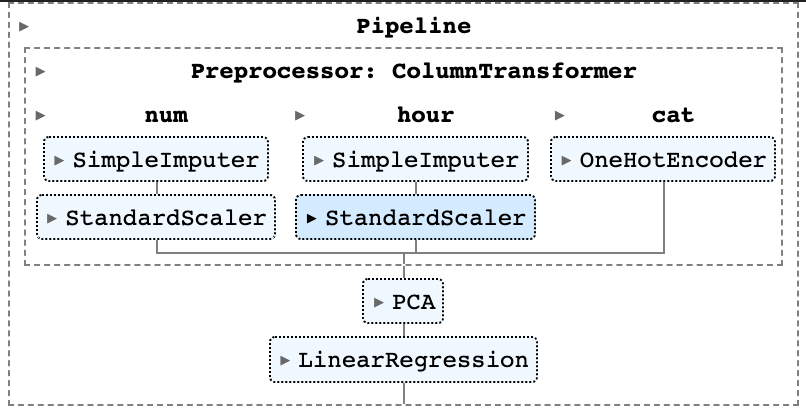
위 코드를 통해, 그림과 같은 Pipeline을 갖는 Principal Component Regression method를 구현할 수 있다. 마찬가지로, sklearn.cross_decomposition의 PLSRegression을 이용하여 다음과 같은 PLS 파이프라인을 생성할 수 있다.
PLS
# PLS
from sklearn.cross_decomposition import PLSRegression
pls = Pipeline(
steps=[("Preprocessor",preprocessor_1),
('PLS', PLSRegression(n_components=3))]
)
pls.fit(X_train, y_train)
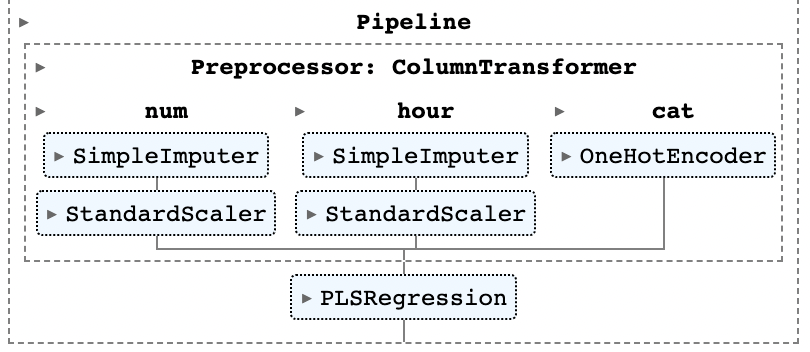
Comparison between PCR / PLS
이제 PCR과 PLS를 비교해보자. 성능 비교 이전에, 우선 validation data를 바탕으로 데이터셋을 첫번째 주성분으로 정사영projection시켜 반응변수의 실제값과 예측값을 scatter plot으로 확인해보도록 하자. 이때 첫 번째 주성분을 택한 이유는 앞서 PCA에서 95.4% 설명력을 갖는다는 것을 확인했기 때문에 가능하다. 혹시 두 번째 성분을 바탕으로 분석하고 싶다면 아래 코드를 쉽게 수정하면 될 것이다. 코드는 다음과 같다.
# PCR vs. PLS plot
pca = pcr[0:2] # Preprocess to PCA
fig, axes = plt.subplots(1, 2, figsize=(10,3))
# PCA vs PCR
axes[0].scatter(
pca.transform(X_val)[:,0], y_val, alpha = 0.3, label = 'True' # alpha as transparaency
) # 1st principal component vs true y
axes[0].scatter(
pca.transform(X_val)[:,0], pcr.predict(X_val), alpha = 0.3, label = 'Pred'
) # 1st principal component vs pred y
axes[0].set(
xlabel="Projected X_val onto first PCA component", ylabel='y', title = 'PCR / PCA'
)
axes[0].legend()
# PLS
axes[1].scatter(
pls.transform(X_val)[:,0], y_val, alpha = 0.3, label = 'True'
)
axes[1].scatter(
pls.transform(X_val)[:,0], pls.predict(X_val), alpha = 0.3, label = 'Pred'
)
axes[1].set(
xlabel="Projected X_val onto first PCA component", ylabel='y', title = 'PLS'
)
axes[1].legend()
plt.tight_layout()
plt.savefig('plots/pcr_vs_pls.png', transparent=False, facecolor = 'white')
첫 줄의 pca는 PCR 파이프라인에서 Linear Regression을 제외한 PCA까지의 프로세스만 분리한 또다른 파이프라인이다. 코드를 실행하면 다음과 같은 두 plot을 얻을 수 있는데, 왼쪽은 PCA를 통해 얻은 분포와 PCR을 통해 얻은 예측값의 분포를 보이며, 오른쪽은 PLS를 통해 얻은 분포와 예측값의 분포를 나타낸 것이다.
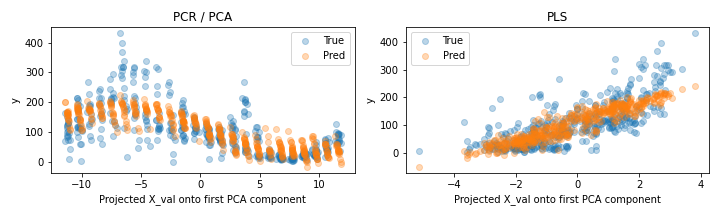
그림으로만 보면 성능이 쉽게 구분되지 않으므로, validation data에 대한 R-squared value와 RMSE value를 모두 비교해보도록 하자. 각 pipeline의 경우 모두 Regression model 이고, .score 메서드로 결정계수 $R^2$를 얻을 수 있다.
from sklearn.metrics import mean_squared_error
# R_squared
print(pcr.score(X_val, y_val).round(3)) # PCR = 0.544
print(pls.score(X_val, y_val).round(3)) # PLS = 0.617
# RMSE
print(np.sqrt(mean_squared_error(y_val, pcr.predict(X_val))).round(3)) # PCR = 54.958
print(np.sqrt(mean_squared_error(y_val, pls.predict(X_val))).round(3)) # PLS = 50.374
비교 결과, $R^2$ 측면에서는 PCR이 우수한 것으로 파악되었다. 반면 RMSE 측면에서는 PLS가 더 우수한 값을 가지는 것으로 파악되었는데, 이는 이전까지 shrinkage method, model selection을 통해 얻은 RMSE값들보다 더욱 우수한 값이다 (의미있는 진전😃).
References
- scikit-learn 공식 문서 : https://scikit-learn.org/stable/auto_examples/cross_decomposition/plot_pcr_vs_pls.html
Leave a comment