Markov Chain Monte Carlo
Markov Chain Monte Carlo
MCMC라고도 하는 Markov Chain Monte Carlo 기법은 확률분포에서 샘플을 추출하는 여러 종류의 알고리즘을 일컫는다. 다양한 머신러닝 이론들이 등장하며, 기존 통계학에서 다룰 수 없을 정도의 수만-수백만 개의 변수 및 파라미터를 사용하는 모델들 역시 등장했고, 특히 신경망과 같은 모델들은 너무나도 널리 사용되고 있다. 하지만 그러한 고차원 모델들에 대해 샘플링을 수행하거나, 기댓값 등 적분값을 구하는 과정은 기존의 다중적분으로는 불가능하다. 이를 해결하기 위해 몬테카를로 방법, 그중에서도 마코프 체인을 이용한 MCMC가 사용되며 이는 근래 통계학 및 머신러닝 분야에서 매우 중요한 부분을 차지한다.
Markov Chain
Markov Chain은 시간($t$)에 따라 변화하는 시스템(계)의 상태를 설명하기 위한 개념이다. 어떤 시스템의 상태가 A에서 B로, B에서 C로 시간($t=0,1,2,\dots$)에 따라 변화하는 과정이 각각 확률로 주어지는 것을 의미한다. 만일 시간 $t$에서의 상태를 모두 포함하는 충분통계량 $x_t$가 존재하며, 모든 과거의 상태가 이에 포함된다면 이를 markov property라고 한다. 즉, 다음을 의미한다.
\[p(x_{t+\tau}\vert x_t,x_{1:t-1}) = p(x_{t+\tau}\vert x_t)\]Markov property가 만족될 경우 유한한 확률과정열을 다음과 같이 쓸 수 있는데,
\[p(x_{1:T}) = p(x_1)\prod_{t=2}^Tp(x_t\vert x_{t-1})\]이를 Markov Chain 이라고 한다.
Stationary Markov Chain
다음과 같이 time-shift가 이루어져도 joint distribution이 일치하는 markov chain을 stationary markov chain이라고 한다.(stationary : 정상성)
\[\Pr(x_0 = z_0, x_1=z_1,\ldots,x_k = z_k)=\Pr(x_n=z_0,\ldots,x_{k+n}=z_k)\]또한 stationary markov chain에서의 marginal distribution, 즉 $\Pr(x_0=x)$을 해당 마코프 체인의 stationary distribution이라고 한다.
Monte Carlo Integration
몬테카를로 적분은 확률변수의 기댓값, 즉 적분값을 random sampling으로 근사하는 방법이다.
\[\mathrm E[f(x)] = \int f(x)p(x)dx\]확률변수 $X\in\mathbb R^n$ 와 target distribution $p(X)$에 대해 기댓값을 구하기 위해서는 위와 같은 적분을 계산해야 한다. 그러나, 때로는 적분의 closed form을 구하기 어렵거나 데이터가 고차원인 경우 계산 과정이 매우 복잡하여 computation cost 문제가 발생할 수 있다. 이를 극복하기 위해 다음과 같이 적분값을 근사하는 방법을 Monte Carlo integration이라고 한다.
\[\mathrm E[f(x)]\approx {1\over n_s}\sum_{n=1}^{n_s} f(x_n)\]MCMC
Markov Chain Monte Carlo(이하 MCMC)는 몬테카를로 방법 중에서 가장 널리 사용되는 기법 중 하나이다. MCMC의 기본적인 아이디어는 상태공간 $\mathcal X$에서 target density $p^{\ast}(x)$를 stationary distribution으로 하는 마코프 체인을 구성하는 것이다. 이는 상태공간에서 각 상태 $x$에 머문 시간($t$)의 비율이 $p^{\ast}(x)$에 비례하도록 random walk를 진행하는 것을 의미한다.
이러한 random walk로부터 샘플 $x_0,x_1,\ldots$를 추출하여 확률측도 $p^{\ast}$에 대해 몬테카를로 적분을 실행할 수 있다. 이때 중요한 것은, random walk의 초기 과정은 sample의 개수가 적기 때문에 이때에는 정상성(stationarity)이 보장되지 않는다. 따라서 정상성에 이르는 시간동안의 샘플은 제거하는 것이 맞으며, 정상성에 이르기까지의 시간을 burn-in time이라고도 한다.
MH(Metropolis Hastings) Algorithm
MCMC 알고리즘의 가장 대표적인 것 중 하나인 MH 알고리즘에 대해 살펴보도록 하자. 앞서 MCMC의 기본 원리는 상태간 이동이 정상분포($p^{\ast}$)에 근거해 이루어진다고 설명한 바 있다. MH 알고리즘에서는 $x\to x’$의 상태이동이 확률 $q(x’\vert \;x)$ 로 이동하는데, $q$는 proposal distribution 이라고 한다(새로운 상태 $x’$로 움직일 것을 제안받는다는 의미로 proposal이라고 하는 것 같다😃).
알고리즘에서 $x\to x’$로의 상태 이동을 제안받으면, 그 제안을 accept 할 것인지 결정하는 과정이 존재한다. Accept가 이루어지면 $x’$를 새로운 샘플로 사용하고, 그렇지 않으면 기존 샘플을 반복해서 추출한다. 전체 알고리즘은 다음과 같다.
Metropolis Hastings Algorithm
Initialize $x^0$
각 단계 $s=0,1,2\ldots$ 에 대해 다음 과정을 반복한다:
1) $x=x^s$
2) $x’\sim q(x’\vert x)$ 으로부터 새로운 샘플을 추출한다.
3) Acceptance probability를 계산한다.
\[\begin{aligned} \alpha&=\frac{\tilde p(x')q(x\vert x')}{\tilde p(x)q(x'\vert x)}\\ A&=\min(1,\alpha)\end{aligned}\]4) $u\sim U(0,1)$ 으로부터 샘플을 추출한다.
5) 새로운 샘플 $x^{s+1}$을 다음과 같이 정의한다.
\[x^{s+1}=\begin{cases}x'\;\;:\;\mathrm{if} \; u\leq A\;\;(\mathrm{accept}) \\ x^s\;\;:\;\mathrm{if}\; u>A\;\;(\mathrm{reject}) \end{cases}\]
여기서 $p^{\ast}(x) = \tilde p(x)/Z$ 로 $\tilde p $는 정규화되지 않은 분포를, $p^{\ast}$는 정규화상수를 이용하여 정규화된 분포를 각각 나타낸다.
MH 알고리즘이 실제로 정상확률분포 $p^{\ast}$로부터 샘플을 생성한다는 것을 증명하는 자세한 과정은 참고 교재를 살펴보면 좋을 것 같다. 아래는 실제로 MH 알고리즘을 이용한 sample generating을 코딩해보도록 하겠다.
Code
앞서 살펴본 MH 알고리즘에서, proposal distribution을 simple normal distribution $N(0,1)$ 로 하는 코드를 구현해보도록 하자. 필요한 패키지들은 다음과 같다.
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
샘플링하고자 할 타겟 분포를 이번에는 평균이 5, 표준편차가 10인 정규분포로 하고, 다음과 같이 random variable을 scipy.stats 으로 설정했다.
# Parameter
MU = 10.0
SIGMA = 5.0
target = ss.norm(loc=MU, scale=SIGMA) # target distribution
MH 알고리즘은 아래와 같은 코드로 진행시켰다. 총 반복횟수는 10000회로 둔 뒤 초기값은 임의로 설정했고(3.0, random으로 생성해도 된다) 각 반복문의 단계에서 이전 state에 proposal distribution을 더한 값 x_proposed으로 $A$ 값을 계산하여, uniform distribution에서 추출한 $u$와 비교한 뒤 새 단계의 state를 업데이트 하는 방식이다.
# Rep count = 10000
x = np.zeros(shape=10000)
# initialize x_0
x[0] = 3.0
for i in range(1,10000):
x_t = x[i-1]
x_proposed = x_t + np.random.standard_normal(1)[0] # Proposal Distribution
A = min(1, target.pdf(x_proposed) / target.pdf(x_t)) # Since q is symmetric
u = np.random.uniform(size=1)[0] # u from Uniform dist
if u <= A : # Accept
x[i] = x_proposed
else:
x[i] = x_t
Plotting한 결과는 다음과 같다.
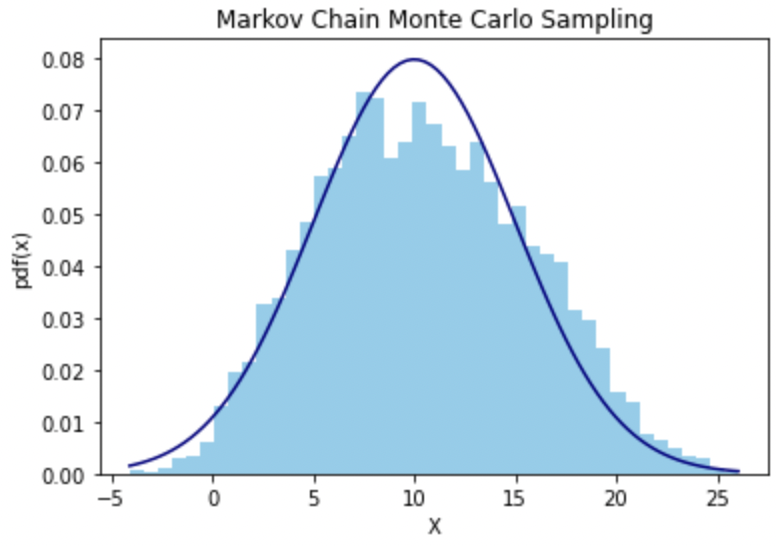
References
- Probabilistic Machine Learning : Advanced Topics, Murphy.
- Code at github
Leave a comment