이진 트리(Binary Tree)
이진 트리
트리

트리Tree 혹은 트리형 자료구조란, 그래프의 일종으로 부모노드-자식노드의 관계로 자료 구조를 표현한 것을 말한다. 위 그림과 같이 초기 시작노드Root Node(빨간색 테두리 노드)를 기반으로 아래로 자식노드와 그들의 자식노드를 순차적으로 표현한다. 트리 노드의 특징은, 서로 다른 두 노드를 연결하는 경로가 유일하게 존재한다는 것이다.
트리형 자료구조를 사용하는 주된 이유는, 구조에서부터 유추할 수 있듯이 데이터를 효과적으로 탐색하기 위함이다. 오히려, 단순히 데이터를 저장하기 위해서는 각 노드의 연결관계를 저장해야한다는 점에서 비효율적일 수 있다.
순회Order
순회란, 트리형 자료구조에 대해 각 노드를 어떤 순서로 탐색할 지를 의미한다. 노드를 탐색하는 순서에 따라 전위 순회, 중위 순회, 후위 순회의 세 가지로 분류된다. 각 순회의 방법은 다음과 같다.
전위 순회 : 시작 노드 > 왼쪽 서브트리 > 오른쪽 서브트리 중위 순회 : 왼쪽 서브트리 > 노드 > 오른쪽 서브트리 후위 순회 : 왼쪽 서브트리 > 오른쪽 서브트리 > 노드
이진 트리
이진 트리란, 트리형 자료구조에서 각 노드가 최대 2개의 자식 노드child node를 가지는 트리를 의미한다.
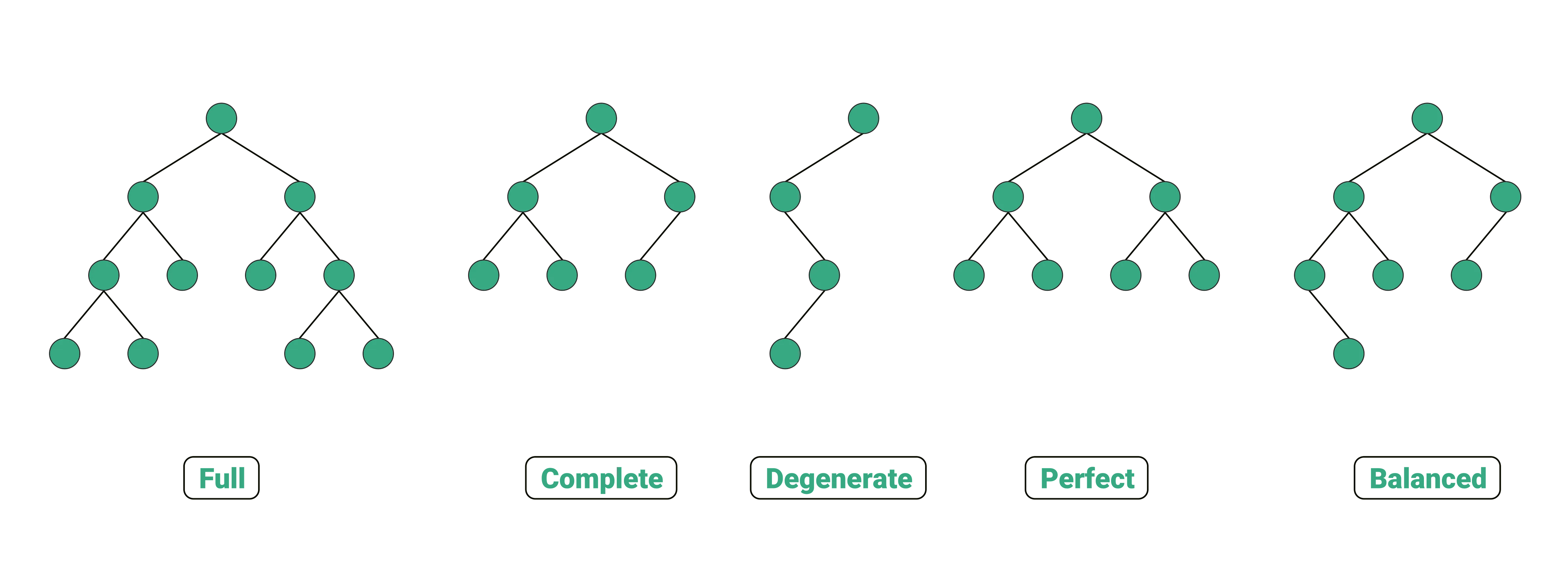
이진 트리의 종류로는 위 그림과 같은 것들이 있다. 포화 이진 트리Full binary tree는 leaf node(트리 가장 하단부의 노드)를 제외한 나머지 노드들의 차수가 2인 경우를 의미한다. 또한, 포화 이진 트리에서는 다음이 성립한다.
\[\text{Number of Leaf Nodes} = \text{Number of Internal Nodes} + 1\]완전 이진 트리Complete binary tree란, 포화 이진 트리와 같이 구성되지만, 각 단계에서 왼쪽 트리부터 채워지는 경우를 의미한다. 힙(Heap) 자료구조는 완전 이진 트리의 일종이다.
이진 탐색 트리
이진 탐색 트리Binary Search Tree란, 이진 탐색을 위한 이진 트리 기반의 자료구조이다. 아래 그림과 같이 이해하면 되는데, 그래프의 특정 노드를 찾기 위해 이진 트리를 생성한 후 이진 탐색을 기반으로 노드를 찾아나간다.
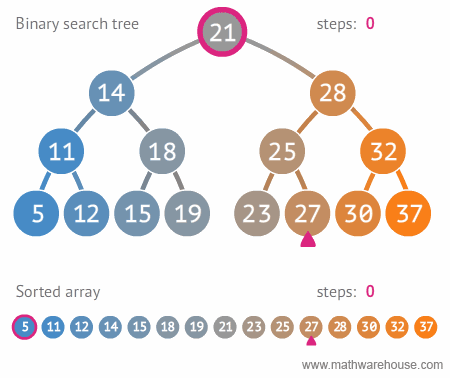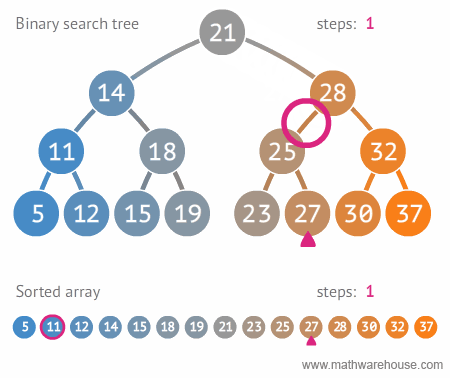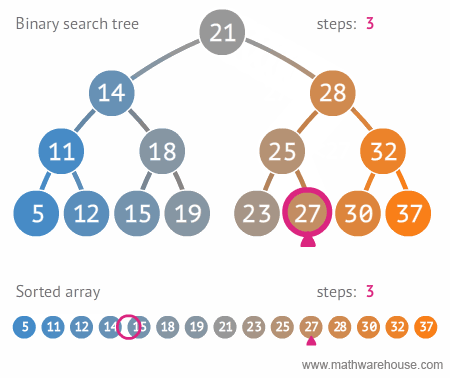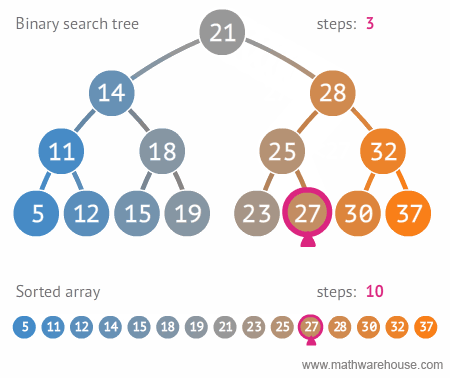
예제
References
- https://towardsdatascience.com/5-types-of-binary-tree-with-cool-illustrations-9b335c430254
- https://velog.io/@kimdukbae/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%A6%AC-Tree
- https://en.wikipedia.org/wiki/Tree_(data_structure)
Leave a comment